Random Art, Revisited

In a previous article, we played around with implementing a tiny programming language for generating random art. In that article and the accompanying code, we implemented a trick I learned from this post, specifically matklad’s response. In learning more about programming language implementation, I came across this wonderful post by Professor Adrian Sampson, which examines the effects of flattening the abstract syntax tree of a similar little language. I thought it’d be interesting to perform a similar analysis with our random art language implementation, so I put together a Rust project with four different implementations.

Implementations

The first implementation is the most basic, where we represent our AST directly:

enum Expr {
    X,
    Y,
    SinPi(Box<Expr>),
    CosPi(Box<Expr>),
    Mul(Box<Expr>, Box<Expr>),
    Avg(Box<Expr>, Box<Expr>),
    Thresh(Box<Expr>, Box<Expr>, Box<Expr>, Box<Expr>),
}

As mentioned last time, it can be more efficient store a single pointer (i.e. Box), which my code confusingly calls the “branch” version (apologies, but I wanted the names to be in alphabetical order and it was the best I could come up with). In this version, the main Expr looks like

enum Expr {
    X,
    Y,
    SinPi(Box<Expr>),
    CosPi(Box<Expr>),
    Mul(Box<Mul>),
    Avg(Box<Avg>),
    Thresh(Box<Thresh>),
}

where each of the intermediate structures looks like struct Mul(Expr, Expr), etc.

After that, we move to a flat version similar to the one explored in Dr. Sampson’s post. In this, we go back to the basic structure, wherein we store (potentially) multiple things in a single Expr variant:

enum Expr {
    X,
    Y,
    SinPi(ExprRef),
    CosPi(ExprRef),
    Mul(ExprRef, ExprRef),
    Avg(ExprRef, ExprRef),
    Thresh(ExprRef, ExprRef, ExprRef, ExprRef),
}

This time, though, the ExprRefs are instead indices, 32 bit unsigned integers, like struct ExprRef(u32). We then use a pool of expressions, struct ExprPool(Vec<Expr>); during its construction, every ExprRef index points to a valid index into this vector. This controls memory layout even more tightly than our branch version, though interpretation still uses an additional vector of the same length.

The final version follows this comment by Bob Nystrom, modifying our flat version to implement a stack-based bytecode interpreter. Every subexpression is interpreted before larger expression that uses it, and the ordering of items is all that matters. We can eschew any kind of pointing or indexing, and move directly to a stack of individual instructions:

enum Expr {
    X,
    Y,
    SinPi,
    CosPi,
    Mul,
    Avg,
    Thresh,
}

These are then stored in order in a struct ExprPool(Vec<Expr>) during construction, and interpretation uses a single stack.

Do you even bench(mark)?

For benchmarking, for each version we build up a random expression of “depth” 26 in the same fashion as last post, then evaluate that expression with a pseudorandomly chosen x and y. Reaching for the amazing hyperfine to time our various approaches:

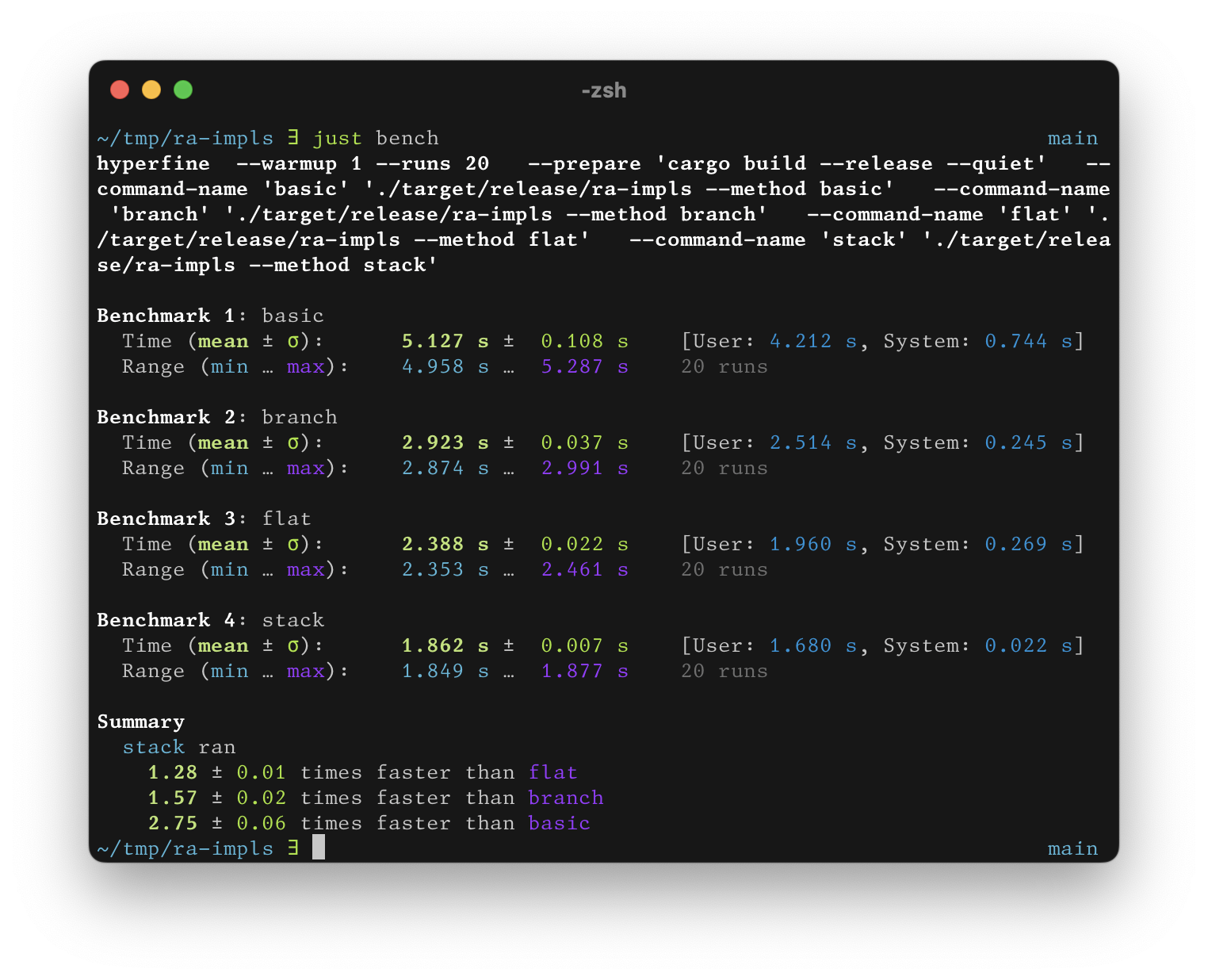
We get the following times:

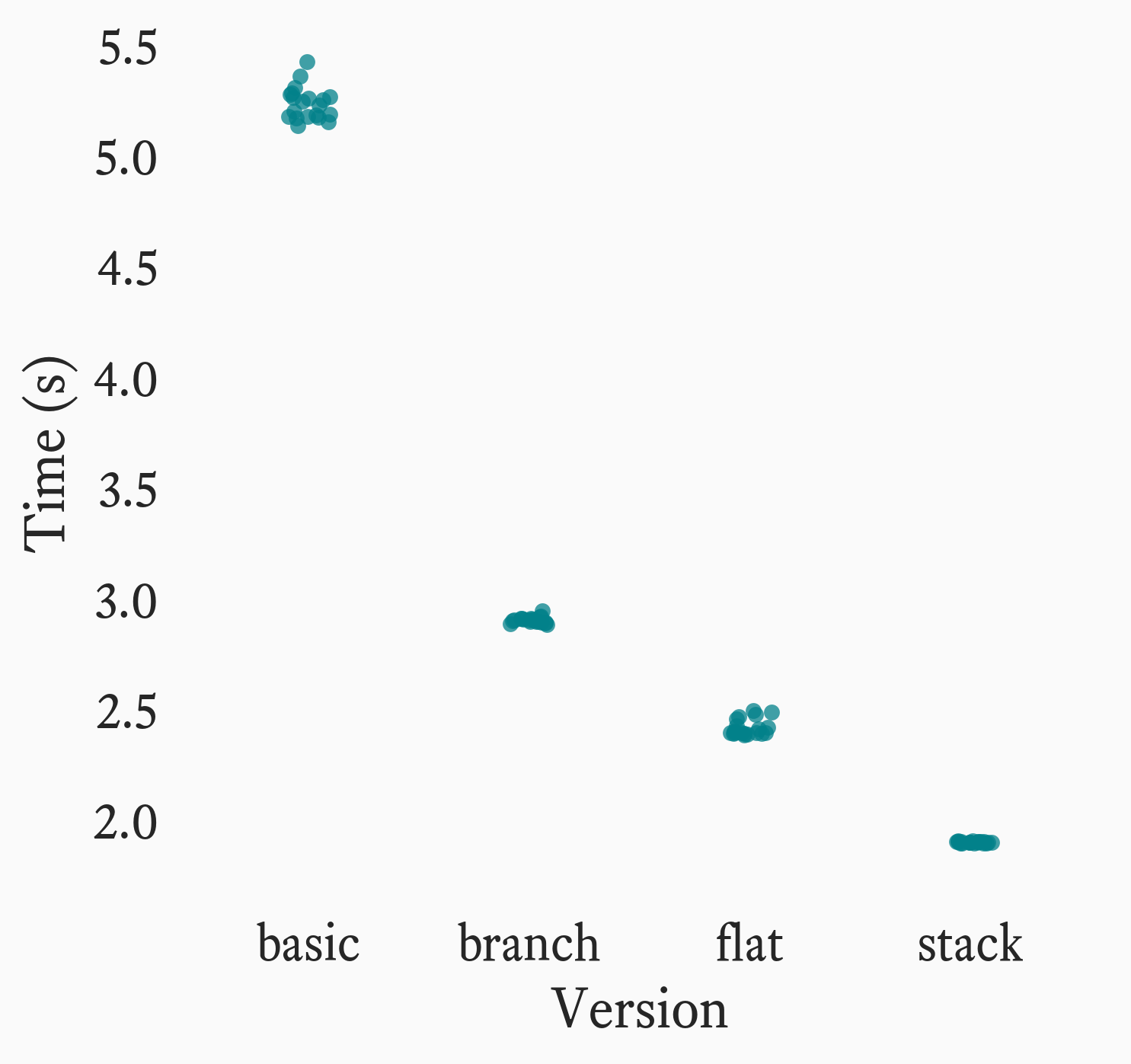
Interestingly, there’s a large time improvement in moving from the basic to the branch version alone! From there, we get further improvements moving to the flat and stack versions, though the savings are less dramatic.

To keep myself honest, I also double-checked that versions yield equivalent results (at least, up to a certain depth) via some property-based tests with the help of the exceptional proptest crate.

Coda & Code

As always, it was fun and interesting to take the lessons learned in reading and see their impacts in practice. Please feel free to check out the code for more details!